The Phantom Troupe wants to sabotage Santa's workshop! To start, they begin by scouting out the area, and discover that it's made up of ~N~ factories numbered from ~1~ to ~N~ with ~M~ bidirectional conveyer belts between them. Due to the workshop's advanced security technology, the Phantom Troupe can only afford to destroy one conveyer belt. However, this might be enough! If the destroyed bridge disconnects the factories, then Santa's workshop will no longer work. Can you find the number of conveyer belts that the Phantom Troupe can destroy to disconnect the workshop?

Santa's workshop is considered disconnected if there is some pair of factories that cannot reach each other via some path of working conveyer belts

Note: The intended solution for the second subtasks uses topics not yet covered in the lessons this year

Constraints

Subtask 1 [80%]

~1\le N\le 5000~

~1\le M\le 5000~

Subtask 2 [20%]

~1\le N\le 2\times 10^5~

~1\le M\le 2\times 10^5~

Input Specification

The first line contains two integers, ~N~ and ~M~.

The next ~M~ lines each contain two integers, ~a_i~ and ~b_i~, indicating a conveyer belt between node ~a_i~ and ~b_i~. Each unordered pair ~(a_i, b_i)~ is unique.

Output Specification

One integer: the number of conveyer belts that the Phantom Troupe can destroy to disconnect the workshop

Sample Input

6 6
1 2
1 3
2 4
3 5
5 1
4 6

Sample Output

3

Sample Explanation

The graph looks like this:

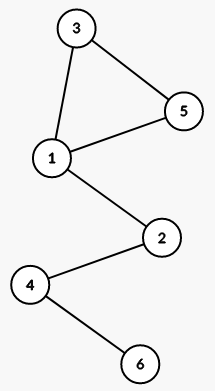
There are 3 conveyer belts that can be destroyed to disconnect the workshop: 1 2, 2 4, and 4 6.