As a Toronto resident for most, if not all of your life, you know that this city is notorious for its bad traffic and constant construction. Toronto has ~N~ intersections and ~M~ roads connecting those intersections. You live at intersection ~B~, and for the next ~Q~ days, you will either drive to a building located at a different intersection, or Toronto closes a road. However, the construction is seemingly going to take longer than ~Q~ days, so these roads will stay closed for the entire input. Is it possible to drive to every destination you want to arrive at?

Constraints

~1 \leq N,M,Q \leq 10^5~

~1 \leq B,a_i,b_i \leq N~

Subtask 1 [30%]

~1 \leq N,M,Q \leq 200~

Subtask 2 [70%]

No further constraints.

All ~S_i~ are unique and consist of only lowercase and capital ASCII characters, numbers, _, and no spaces. The length of all ~S_i~ are at most 20 characters long.

Input Specifications

The first line will contain three space-separated integers, ~N~, ~M~, and ~B~.

The next ~M~ lines will contain the integers ~a_i~, ~b_i~, followed by the string ~S_i~. ~a_i~ and ~b_i~ indicate there is a road connection between these two intersections, and ~S_i~ indicates the name of the road.

The next line will contain the integer ~Q~.

The next ~Q~ lines will queries of the type:

• c R, indicating road ~R~ has been closed for construction, or
• t I, indicating you want to travel from your current intersection to intersection ~I~ (~1 \leq I \leq N~). ~I~ is always distinct from the current intersection.

Output Specifications

For every query of the type t I, output yes if it is possible to travel from to intersection ~I~ or 401 time... otherwise. After every query of this type, you will end up at intersection ~I~ for the next query regardless if it is possible to reach intersection ~I~.

Sample Input 1

6 6 2
1 2 A
2 3 B
2 4 C
3 4 D
4 5 E
5 6 F
5
t 6
c D
t 3
c A
t 1

Sample Output 1

yes
yes
401 time...

Sample Case 1 Explanation

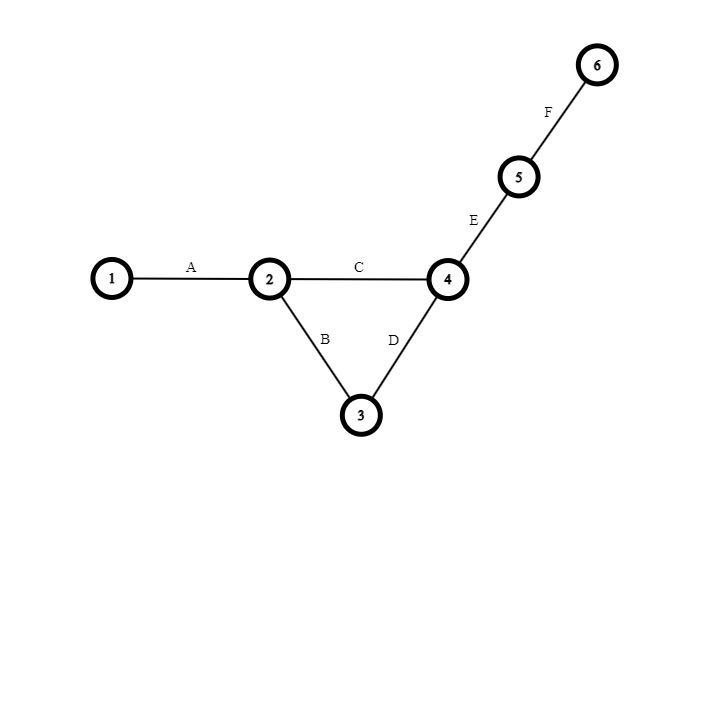
You can travel to intersection 6 via C -> E -> F.

After road D closes, you can still travel to intersection 3 via F -> E -> C -> B.

After road A closes, intersection 1 becomes disconnected from the rest of the city, and is inaccessible.

Here is the graph of the sample test case above:

Sample Input 2

18 27 1
1 2 Steeles_Ave_1
2 3 Steeles_Ave_2
3 4 Steeles_Ave_3
4 5 Steeles_Ave_4
5 6 Steeles_Ave_5
7 8 Finch_Ave_1
8 9 Finch_Ave_2
9 10 Finch_Ave_3
10 11 Finch_Ave_4
11 12 Finch_Ave_5
13 14 Sheppard_Ave_1
14 15 Sheppard_Ave_2
15 16 Sheppard_Ave_3
16 17 Sheppard_Ave_4
17 18 Sheppard_Ave_5
1 7 Warden_Ave_1
7 13 Warden_Ave_2
2 8 Birchmount_Rd_1
8 14 Birchmount_Rd_2
3 9 Kennedy_Rd_1
9 15 Kennedy_Rd_2
4 10 Midland_Ave_1
10 16 Midland_Ave_2
5 11 Brimley_Rd_1
11 17 Brimley_Rd_2
6 12 McCowan_Rd_1
12 18 McCowan_Rd_2
9
c Steeles_Ave_1
t 8
c Finch_Ave_2
c Birchmount_Rd_2
c Birchmount_Rd_1
t 15
c Kennedy_Rd_2
c Sheppard_Ave_3
t 5

Sample Output 2

yes
yes
401 time...

Sample Case 2 Explanation

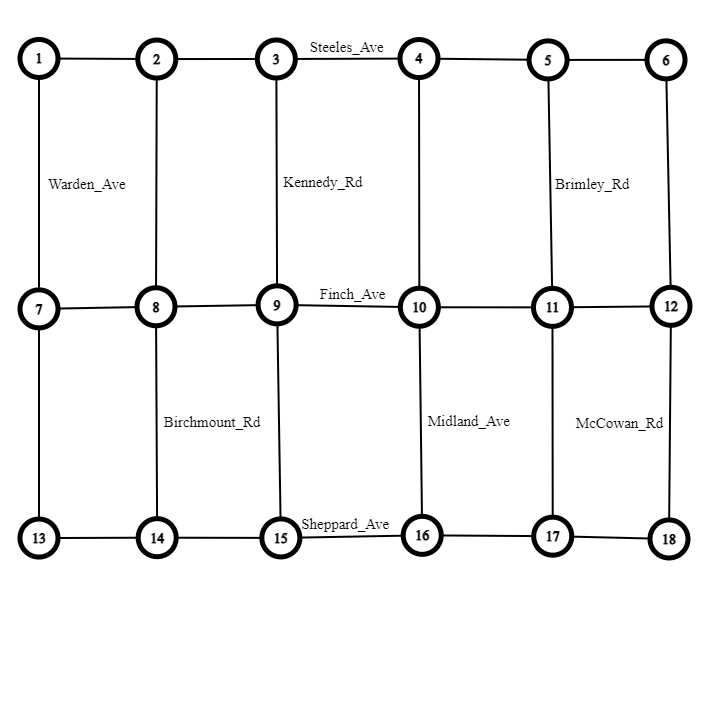
You can travel to intersection 8 by driving South down Warden and then making a left onto Finch.

After a section of Finch and Birchmount closes, you can travel to intersection 15 by driving West down Finch then making a left onto Warden, then making a left onto Sheppard.

After a section of Kennedy and Sheppard closes however, you are now stuck in a part of Scarborough disconnected from the rest! Guess you have to take the 401... (it's going to take you 2 hours trust me on this one)

Here's the map in question: