Santa's assistant, Hatsune Miku, has been tasked with minimizing the cost of a light-up toy! The toy can be described as ~N~ lights numbered ~1~ to ~N~ connected by ~M~ wires, each connecting two lights ~a_i~ and ~b_i~ with a cost ~w_i~. Santa wishes to use some subset of wires to connect all ~N~ lights with minimum total cost. However, there are often multiple ways to do so, and Hatsune Miku doesn't know which configuration Santa will choose. As such, she decides that her task should be to remove all wires that could never be in a minimum configuration. Can you figure out the number of wires that she must keep (i.e. the number of wires that could potentially be part of a configuration that connects all the lights with minimum total cost)?

More formally, you are tasked with finding the number of edges in a graph that could potentially be part of its Minimum Spanning Tree.

Constraints

~1\le N\le 2\times10^5~

~1\le M\le 2\times 10^5~

~1\le a_i, b_i\le N~

~1\le w_i\le 10^8~

It is guaranteed that the graph is connected.

Input Specification

The first line contains two integers ~N~ and ~M~: the number of nodes and edges respectively.

The next ~M~ lines each contain 3 integers ~a_i~, ~b_i~, and ~w_i~, indicating an edge between ~a_i~ and ~b_i~ of weight ~w_i~

Output Specification

One integer, the number of edges that could potentially be part of a Minimum Spanning Tree.

Sample Input

5 6
1 2 2
1 3 2
1 4 4
1 5 4
5 4 4
4 2 5

Sample Output

5

Sample Explanation

The graph looks like this:

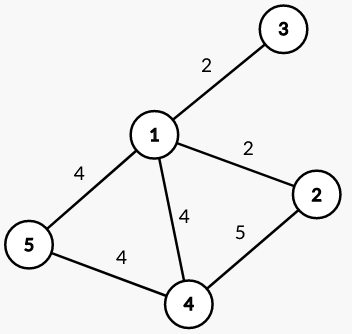
Two potential MST's are drawn below:

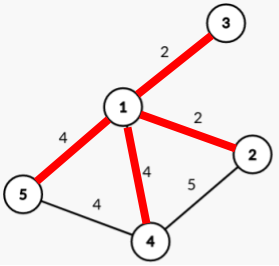
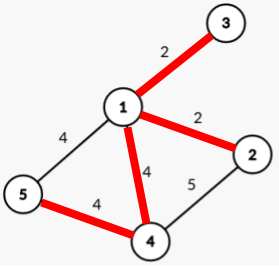
From this, it should be clear that 1 2, 1 3, 1 4, 1 5, and 5 4 can all be used in the MST. However, 4 2 cannot; so, there are ~5~ edgess that could potentially be part of an MST.