Mock Canadian Computing Competition: 2026 Senior #5

In the great white north there was a siting of a mysterious creature known as a yeti. Researchers were immediately notified, and a team of ~N~ searchers were sent to try to find out more about the mysterious yeti. The siting location is a vast snowy land which can be represented as a grid with ~R~ rows and ~C~ columns. Each searcher is placed on one of the edges of the grid, somewhere either on the first or last row or column. One by one, a searcher is released and crosses directly across the grid. It is guaranteed that no two searchers will begin directly across from each other or at the same position.

The searchers are told to look out for footprints that could have been left by the yeti, but unfortunately due to the heavy snowfall, those tracks have faded. The searchers traverse across the grid, however if they encounter the footprints of a previous searcher, they get confused and follow it out of the search grid thinking it was the yeti's footprints. In order to maximize the chances of encountering the yeti, they want to explore the most number of cells possible. What is the maximum number of cells in the grid that can be explored?

Input Specification

The first line contains ~3~ spaced integers, ~N~, ~R~, and ~C~ respectively, where ~1 \le R, \, C \le 10^9~ and ~N \le R + C~.

The next ~N~ lines indicate the positions of the searchers. The ~i^\text{th}~ line contains ~2~ spaced integers, ~s_i~ and ~d_i~.

~s_i~ is the side the ~i^\text{th}~ person starts on. The sides are numbered from ~0~ to ~3~, starting with just above the top row going clockwise.

If ~s_i~ is ~0~ or ~2~, indicating a searcher begins on the top or bottom-most rows, then ~d_i~ represents the number of cells to the left of them on the top/bottom-most row of the grid. These searchers will go directly north or south to the other side of the grid.

If ~s_i~ is ~1~ or ~3~, indicating a searcher begins on the left or right-most rows, then ~d_i~ represents the number of cells north of them on the left/rightmost column of the grid. These searchers will go directly to the side, either left or right to the other side of the grid.

The following table shows how the available 15 marks are distributed.

Marks	Bounds on ~s_i~	Bounds on ~N~
~2~ marks	~0 \le s_i \le 3~	~1 \le N \le 2~
~3~ marks	~1 \le s_i \le 2~	~1 \le N \le 100~
~5~ marks	~0 \le s_i \le 3~	~1 \le N \le 100~
~5~ marks	~0 \le s_i \le 3~	~1 \le N \le 1\,000~

Output Specification

Output the maximum possible number of visited cells in the search grid.

Sample Input 1

2 3 4
0 2
1 1

Output for Sample Input 1

5

Explanation of Output for Sample Input 1

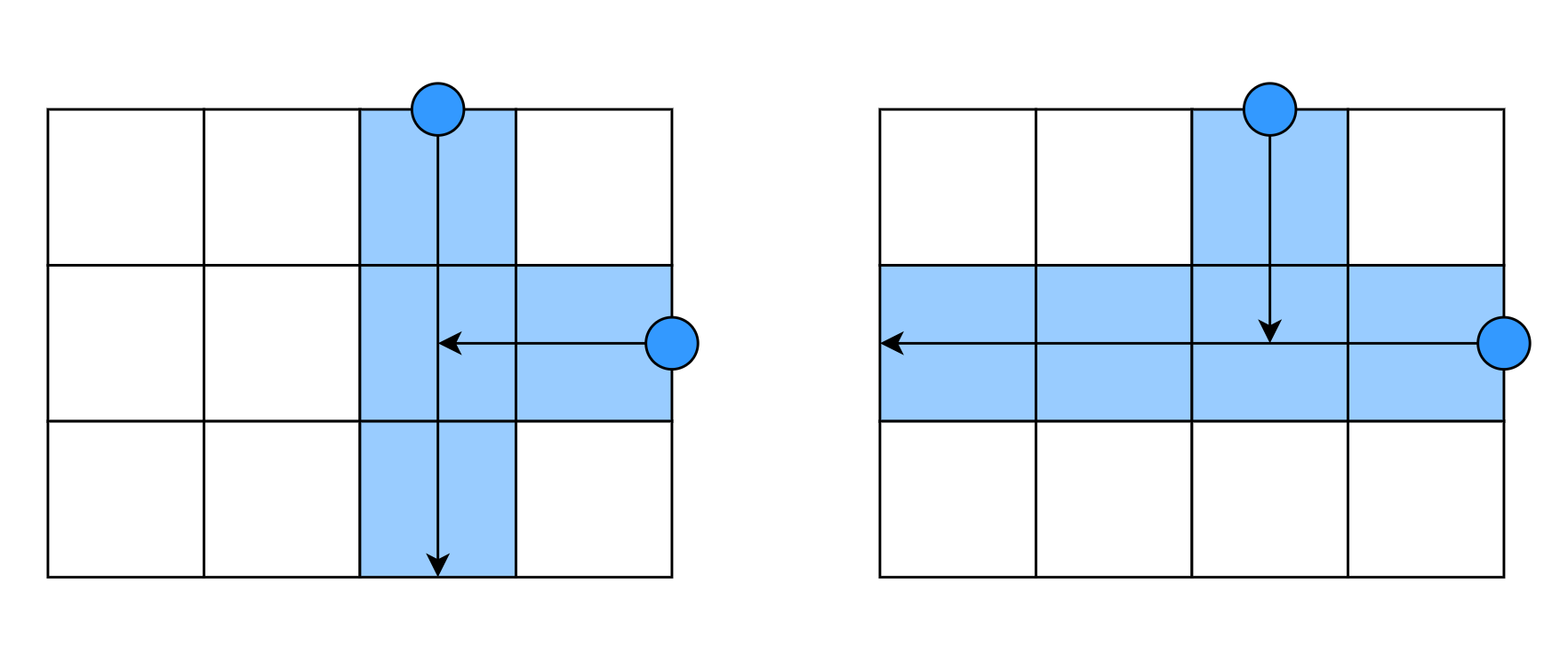
There are 2 searchers, as shown in the diagram below as circles, and there are ~2~ different orderings we could send the searchers. By sending the one on the top side first before the one on the right, a total of ~4~ cells can be visited as shown on the left. However, by sending the one on the right side first, a total of ~5~ cells can be visited, which is the maximum as shown on the right.

Sample Input 2

5 8 8
0 5
1 5
2 3
3 6
3 1

Output for Sample Input 2

27

Explanation of Output for Sample Input 2

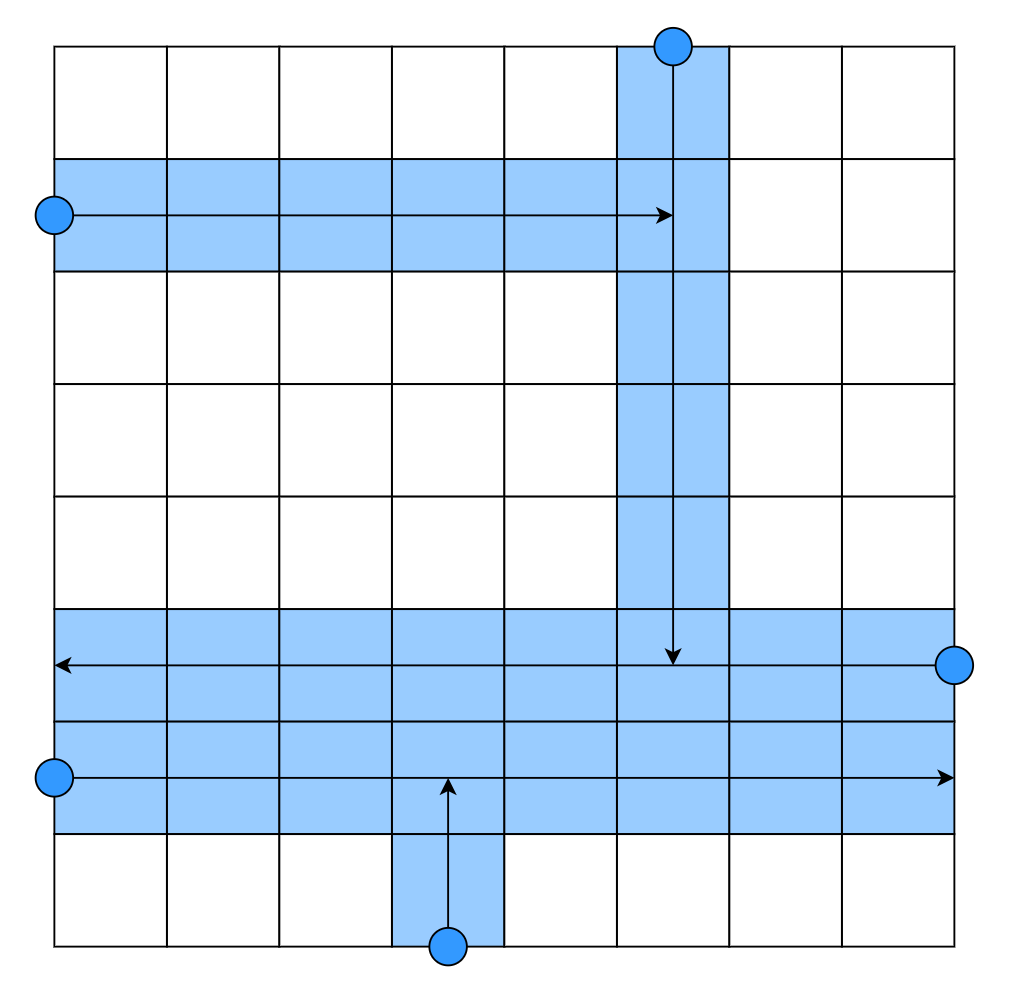
By sending the ~2^\text{nd}~, ~4^\text{th}~, ~3^\text{rd}~, ~1^\text{nd}~, and ~5^\text{th}~ searchers in that order, a total maximum of ~27~ cells can be visited as shown in the diagram below.