Mock Canadian Computing Competition: 2026 Senior #3

You have just been appointed as the new manager of Iaminnocent4298's rail network! The network has ~T~ stations (numbered from ~1~ to ~T~) and ~R~ routes that run between various stations. Scheduling problems created by the previous manager has created extremely long transfer times between train lines. As a result, all passengers on the network choose a path to their destination through the minimum amount of transfers possible, even if it isn't the shortest path possible.

For all routes, the trains run a simple schedule. They begin at the first station on the route, then stop at every station in the given order until they arrive at the last station on the route. The train will then turn around and stop at every station in reverse order until they arrive back at the first station on the route. The trains repeat this schedule indefinitely.

~Q~ new passengers have started using the network, and have asked you how to get from their original station to the destination station. Help them determine the route with the shortest amount of transfers. If there are multiple routes with the same minimum amount of transfers, choose the route with the least amount of stops. It is guaranteed no two routes will have the same minimum amount of transfers and stops.

Input Specifications

The following table shows how the available 15 marks are distributed. Subtasks do not have to be completed in order.

The first line contains the integers ~R,T~, the number routes and stations on the network, respectively.

The next ~R~ lines will contain an integer ~L~, the the number of stations on the route, then ~L~ distinct space-separated integers ~s_i~, the list of stations the train stops at, in order.

The next line will contain the integer ~Q~, the number of new passengers (queries).

The next ~Q~ lines will contain two distinct space-separated integers ~o_i~ and ~d_i~, the original station and the destination station for the ~i^\text{th}~ passenger, respectively.

Marks	Bounds on ~R~	Bounds on ~T~	Bounds on ~Q~	Additional Constraints
~2~ marks	~1 \le R \le 50~	~2 \le T \le 50~	~1 \le Q \le 10~	None
~2~ marks	~1 \le R \le 250~	~2 \le T \le 250~	~1 \le Q \le 100~	All routes have a single common station.
~3~ marks	~1 \le R \le 500~	~2 \le T \le 500~	~1 \le Q \le 250~	Any two routes will have at most 1 station in common.
~8~ marks	~1 \le R \le 1000~	~2 \le T \le 1000~	~1 \le Q \le 1000~	None

For all routes, ~2 \leq L \leq T~. The sum of all ~L~ does not exceed ~2T~.

Output Specifications

For the ~i^\text{th}~ query, output, on a separate line, ~t_i~, the minimum number of transfers required to reach the destination, followed by ~p_i~, the minimum amount of stops. It is always possible to reach the destination station.

Sample Input

5 9
6 1 2 3 5 6 7
2 1 8
3 4 5 7
2 8 9
2 4 9
2
3 9
1 4

Sample Output

2 3
1 4

Sample Case Explanation

The following diagram is an image of the network, with different colours representing different routes:

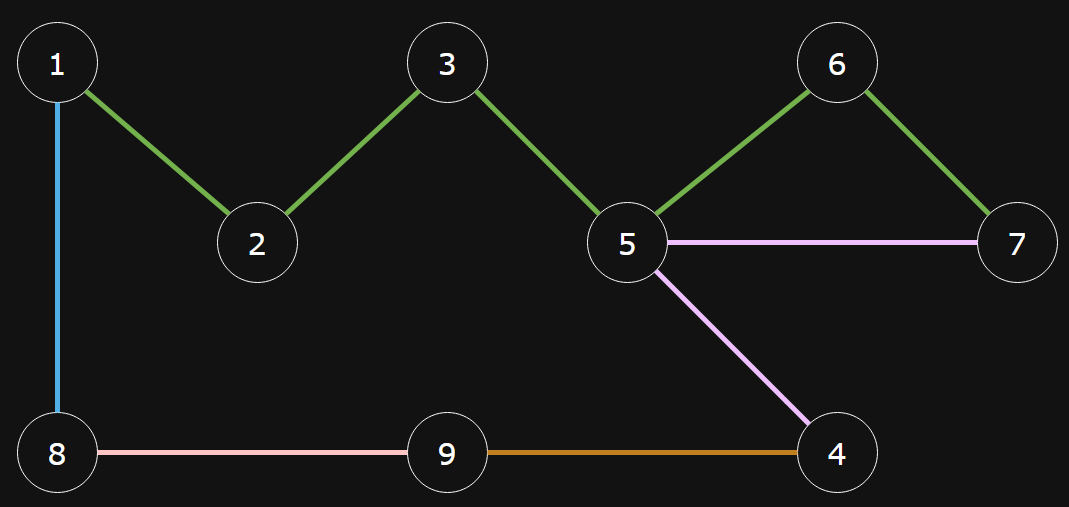
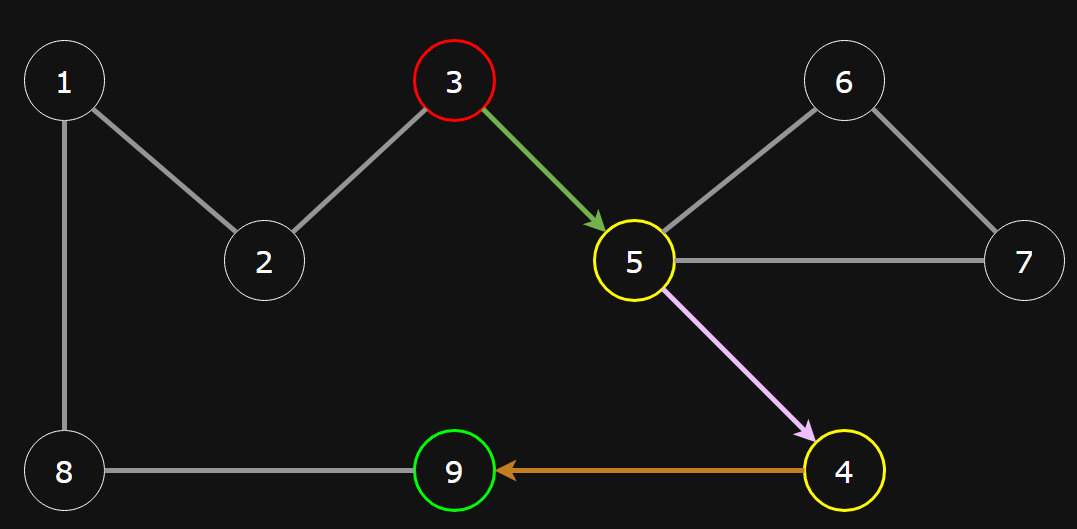
In the first query, the diagram below shows the path with the minimum amount of transfers at 2, and a stop count of 3. Yellow stations are transfers.

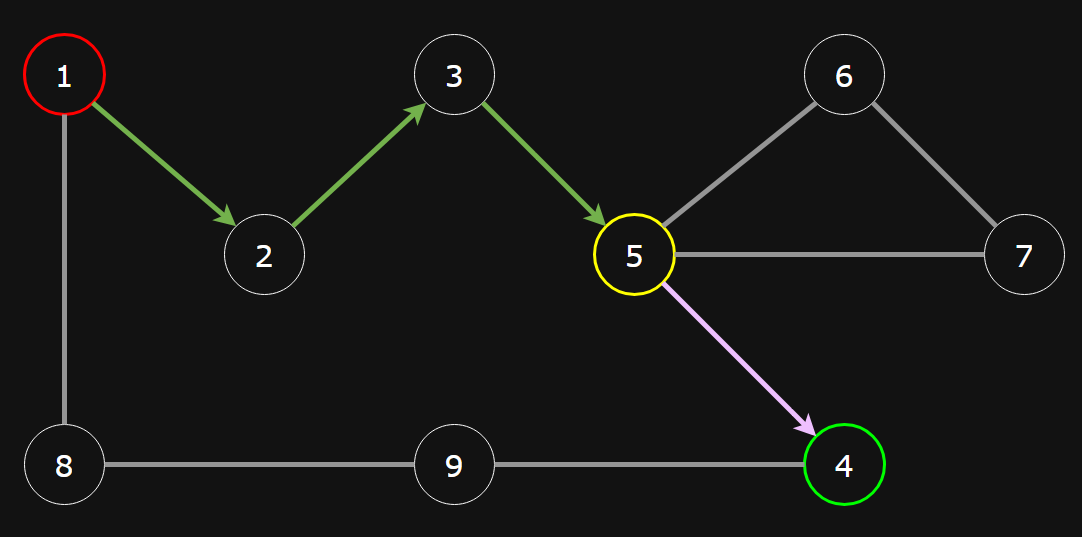
In the second query, the diagram below shows the path with the minimum amount of transfers at 1, and a stop count of 4. Yellow stations are transfers.