Mock Canadian Computing Competition: 2026 Junior #3

Moly the mole lives in a cozy underground room. Moly loves putting up decorations, especially in the form of framed pictures. Over the years, due to Moly's indecisiveness, his wall has become riddled with ~N~ holes from all the drilling he has done to put up and take down pictures. Each of the holes on the wall is given integer coordinates ~(X, Y)~.

Moly takes down all his pictures and decides, "screw it, I will no longer drill new holes and lower my property's value".

He instead wants to screw in just one final, special square-shaped picture where the center of the picture will be located right at the center of his wall (considered ~(0,0)~). The picture will be upright and be axis-aligned.

Moly can choose any square frame size to buy from Froggy's Framing, but there's a catch: Moly can only hang the special frame if at least ~K~ holes on the wall lie exactly on the frame's perimeter (so he can screw in the frame properly).

For example if ~K=2~ and the holes in the wall are at ~(2,-1), (1,2), (0,-2)~, then Moly can screw in ~1~ frame, like this:

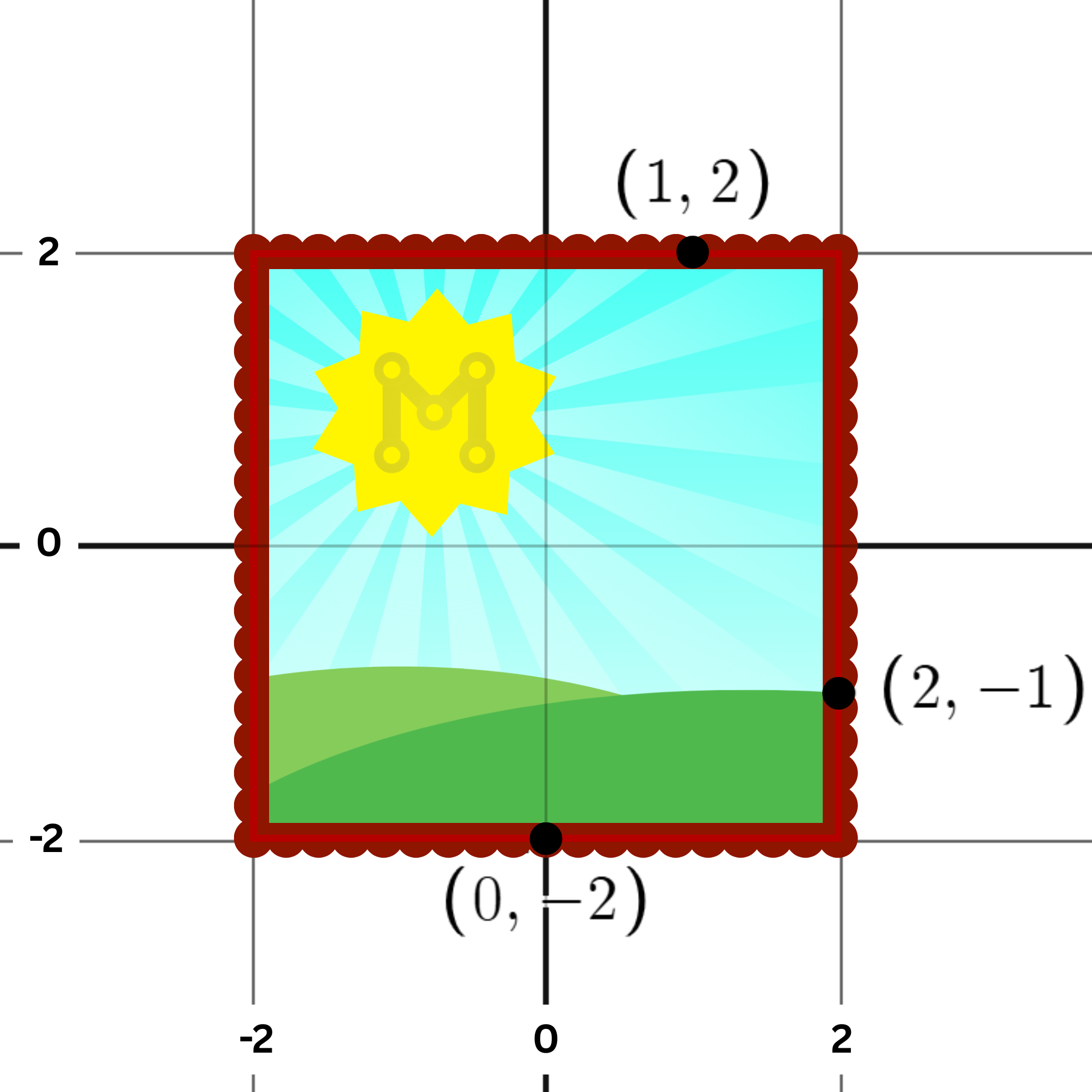
As shown in the diagram, at least ~2~ holes lie on the perimeter when the frame has sides of length ~4~. The center of the frame lines up with the center of the wall.

Given the coordinates of the wall's holes and the number of holes required for the frame to be screwed in, help Moly figure out the number of different square frames sizes he can screw in.

Input Specification

The first line contains ~2~ spaced integers, ~N~ and ~K~, the number of holes on the wall and the least the number of holes required to lie on the frame's perimeter to be able to be used.

The next line ~N~ lines will each contain ~2~ integers ~X_i~ and ~Y_i~ separated by one comma (no spaces). This represents the location of the ~i^\text{th}~ hole. It is guaranteed that every hole occupies a distinct coordinate and that Moly didn't make a hole at ~(0,0)~.

The following table shows how the available 15 marks are distributed.

Marks Awarded	Bounds on ~N~ and ~K~	Bounds on ~X_i~ and ~Y_i~
~2~ marks	~1 \le N, K \le 10~	~-100 \le X_i, Y_i \le 100~
~5~ marks	~1 \le N, K \le 10^{5}~	~-10^{3} \le X_i, Y_i \le 10^{3}~
~8~ marks	~1 \le N, K \le 10^{5}~	~-10^{5} \le X_i, Y_i \le 10^{5}~

Output Specification

Output the number of different frame sizes Moly can use.

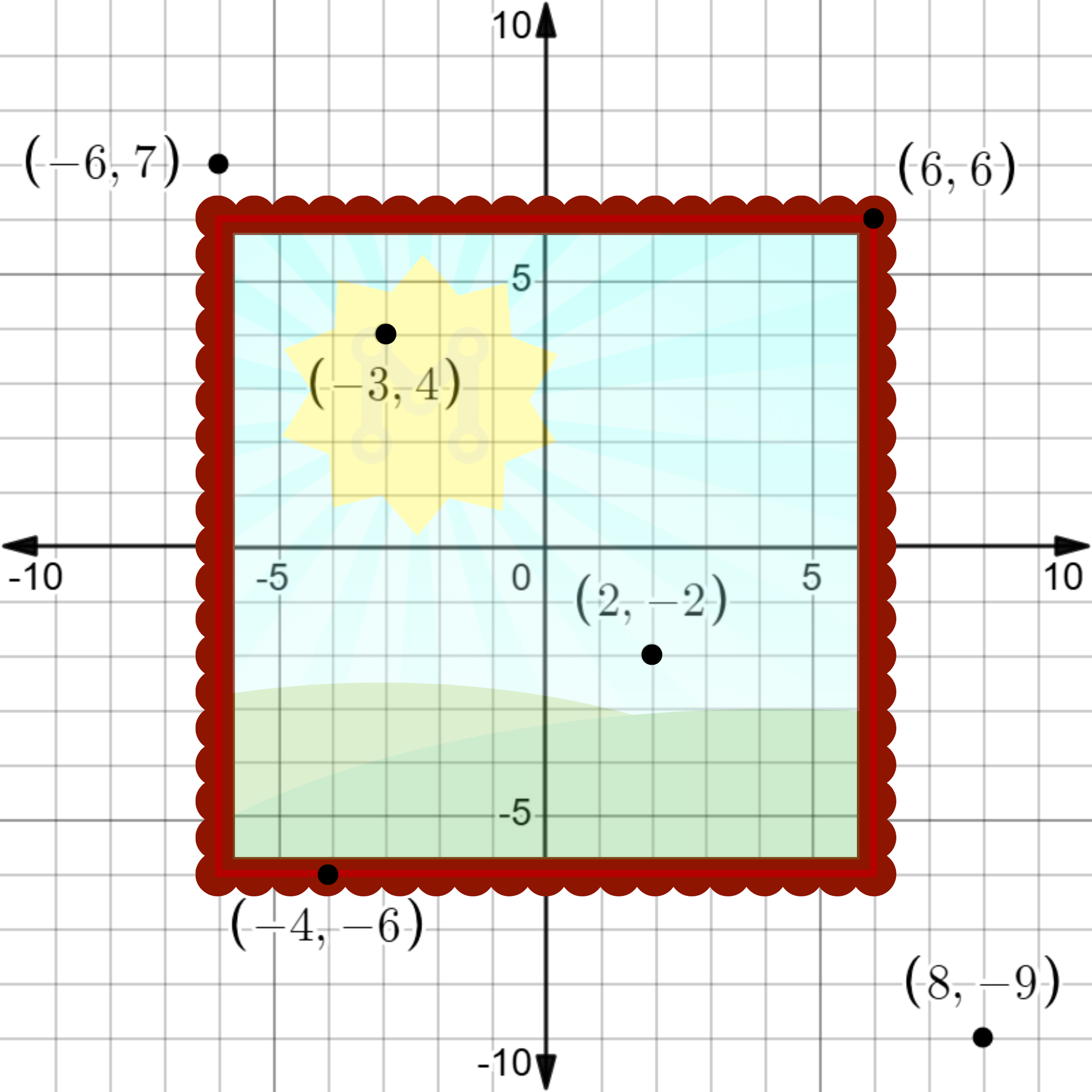
Sample Input 1

6 2
-6,7
6,6
-3,4
2,-2
-4,-6
8,-9

Output for Sample Input 1

1

Explanation of Output for Sample Input 1

One possible frame can be used. The frame uses the holes at positions ~(6,6)~ and ~(-4,-6)~.