After becoming the overlord of the new world, Sora realized that it was imperative to optimize the transportation system of his country in order to manage such a big empire. As a new nation, the country is arranged in a very cost efficient manner: There are ~N~ cities, and ~N-1~ bidirectional highways connecting the cities, allowing anyone in one city to reach another city by traversing a series of highways. In order to revamp the transportation, Sora has decided to first invest some amount of time into Research and Development before revising the highways, to perhaps develop technologies to make traversing highways more efficient.

For each highway, if the country invested at least ~a_i~ hours into R&D prior to beginning the rollout, it will take ~r_i~ hours to traverse the highway. Otherwise, it will take ~t_i~ hours to traverse it instead. Furthermore, Sora has set a strict goal for this operation: it should take at most ~K~ hours to traverse from any one city to another. Of course, he would like to minimize the amount of time that he needs to invest in R&D while reaching his goal.

As his dear Shiro, you must find out how many hours he should pour into R&D!

Constraints

In all tasks,

~0<r_i<t_i\le 10^6~

~0\le a_i\le 10^{12}~

~1\le N\le 10^5~

~1\le K\le 10^{11}~

Subtask 1 [30%]

~a_i\le 50~

Subtask 2 [70%]

No additional constraints.

Input Specification

The first line will contain two integers, ~N~ and ~K~.

The next ~N-1~ lines will contain 5 integers, ~x_i~, ~y_i~, ~a_i~, ~r_i~, ~t_i~. The represents a highway joining ~x_i~ and ~y_i~, requiring ~a_i~ hours of R&D to take ~r_i~ hours to traverse, and ~t_i~ hours otherwise.

Output Specification

One integer, the optimal number of hours to put into R&D to ensure that we can traverse between any two cities in at most ~K~ hours. If this is impossible, print out ~-1~ instead.

Sample Input

4 5
1 2 2 1 3
2 3 4 1 2
1 4 2 2 4

Sample Output

2

Sample Explanation

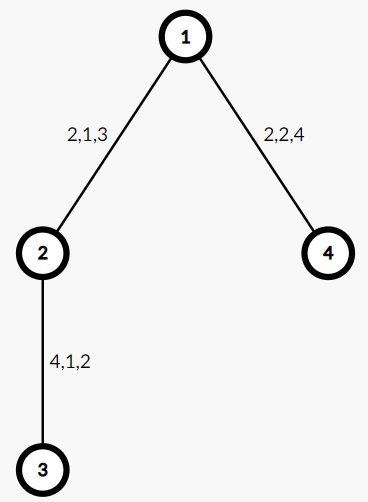
If 2 hours are put into R&D, the longest path has length ~1+2+2=5~. This is less than or equal to ~K~, so it is valid. Any less, and the longest path will have length ~3+2+4=9~. So, it is optimal to invest ~2~ hours into R&D.