Jimmy has planned a trip to the University of Waterloo for their March Break Open House. Now, he needs to convince his friends to go with him.

Jimmy has ~N~ friends numbered ~1~ to ~N~, none of whom wants to go on the trip with him right now. However, Jimmy can bribe the ~i~th friend to go by buying them a gift worth ~a_i~ dollars. In addition, there are ~M~ uni-directional relationships between his friends, numbered ~1~ to ~M~. The ~j~th relationship allows him to deduce that if friend ~u_j~ decides to go on the trip (whether bribed or not), then friend ~v_j~ will decide to go as well of their own volition.

Jimmy would like to convince all of his friends to go to the University of Waterloo with him. Please find the minimum amount of money that he must spend in total to achieve this.

Input Specification

The first line will contain two space-separated integers, ~N~ and ~M~.

The next line will contain ~N~ space-separated integers, ~a_1, a_2, ..., a_N~.

The next ~M~ lines will each contain two space-separated integers, ~u_j~ and ~v_j~.

Output Specification

Output one integer, the minimum total amount of money that Jimmy must spend.

Constraints

In all subtasks,

~2 \le N \le 10^4~

~1 \le M \le 10^6~

~1 \le a_i \le 10^4~

~1 \le u_j, v_j \le N~

~u_j \ne v_j~

Subtask 1 [30%]

There will be no cyclic relationships. In other words, for all friends ~A~ and ~B~, if ~A~ going directly or indirectly leads to ~B~ going, then ~B~ going won't directly or indirectly lead to ~A~ going.

Subtask 2 [70%]

No further constraints.

Sample Input

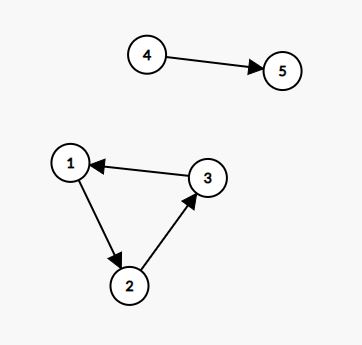
5 4
4 6 5 10 3
1 2
2 3
3 1
4 5

Sample Output

14

Explanation for Sample Output

Jimmy can convince everyone to go by bribing friends ~1~ and ~4~.