LCC '22 Contest 4 S4 - Tourist
View as PDFIn Byteland, there are cities numbered
to
, initially all disconnected. However, every once in a while, the Bytelandian government may decide to add a road between two cities
and
, allowing permanent travel between these two cities from then on.
Additionally, at different points in time, someone may decide to take a trip from their city! Each city is given a prosperity level , and someone leaving city
will want to travel to the city with a strictly higher prosperity level. However, they wouldn't want to feel too inferior, so instead they'll take a tour to the city with the next strictly higher prosperity level.
Your job is to figure out, of all the cities someone can reach, what the closest prosperity level is that's also higher than their current city's prosperity level.
Constraints
Input Specification
The first line contains two integers, and
.
The second line contains integers, the
-th of which denoting
.
The next lines are in one of the following formats:
| Query Type | Structure | Description |
|---|---|---|
| 1 | B a b |
A bridge is built connecting city a and b |
| 2 | T c |
Someone decides to take a trip from city c |
Output Specification
For each query of type 2, output the closest higher prosperity level the person leaving city can reach. If the current prosperity level is maximal, output
-1
Sample Input
5 7
1 2 2 3 4
B 1 2
B 2 4
B 2 3
T 2
B 3 5
T 4
T 1Sample Output
3
4
2Sample Explanation
The first 3 queries build bridges. Here is a model of the graph (note that the node index is followed by the node's prosperity level):
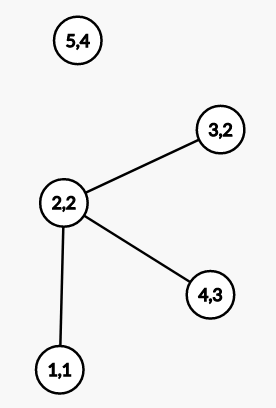
For the fourth query, notice that the second city can reach the fourth city with a prosperity level of .
After building the bridge in the fifth query, the graph looks like such:
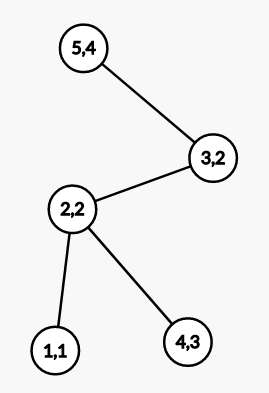
For the sixth query, the fourth city can reach the fifth city with prosperity level .
For the seventh query, the first city can reach a prosperity level of , which is the closest prosperity level that's higher than
.
Comments