Along the palm beaches of Hawaii in the blazing summer are numerous umbrellas. When facing the ocean, the umbrellas appear to be isosceles triangles with one side on the x axis and the other sides will have equal length. Let's take a picture - but before we do that, can you estimate the area of all the umbrellas together?

For this problem, there are ~N~ umbrellas each with one vertex at ~(x_{1i}, 0)~ and another vertex at ~(x_{2i}, 0)~. For each umbrella, its third vertex is at ~(\frac{x_{1i}+x_{2i}}2, y_i)~. You are tasked with finding the area of the union of all the umbrellas (total area, where a region overlapped by multiple umbrellas should only be counted once in total).

Constraints

~1\le N\le 10^5~

~1\le x_{1i}< x_{2i}\le 10^8~

~1\le y_i\le 10^8~

Input Specification

The first line contains ~N~, the number of umbrellas.

The next ~N~ lines each contain 3 integers: ~x_{1i}~, ~x_{2i}~, and ~y_i~, describing the ~i~-th umbrella.

Output Specification

One decimal number, the area of the union of all umbrellas. Your answer will be regarded as correct if it has an absolute or relative error at most ~10^{-3}~

Sample Input

2
1 5 2
3 11 2

Sample Output

11.3333

Sample Explanation

There is a triangle with vertices ~(1,0)~, ~(5,0)~ and ~(\frac{1+5}2,2)=(3,2)~. There is another with vertices ~(3,0)~, ~(11,0)~, and ~(\frac{3+11}2,2)=(7,2)~. A diagram for the triangles is shown below

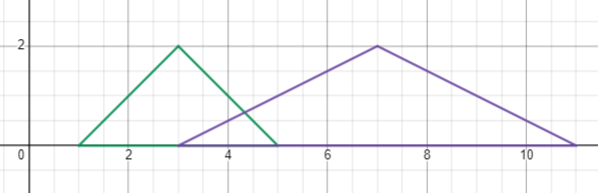
We wish to find this area:

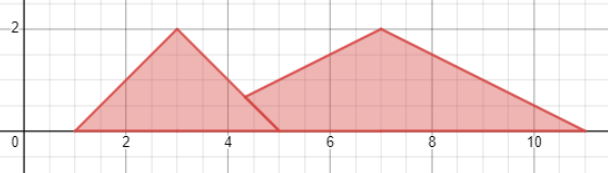
Its area is ~\frac {34}3\approx 11.3333~. If you wish to find the area yourself, note that the two triangles intersect at ~(\frac {13}3,\frac 23)~.