With Christmas steadily approaching, Alex has started planning for his summer job! He plans to first broaden his social network so that he has more options.

Alex has jotted down ~N~ people who he wants to connect with, each of them labelled from 1 to ~N~. He realizes that if he gets in contact with person ~A_i~, they can refer him to person ~B_i~, allowing Alex to connect to person ~B_i~ without having to approach them himself. Similarly, ~B_i~ will also refer Alex to ~A_i~ if Alex connects to them. This referral process takes ~C_i~ days to complete, since both person ~A_i~ and ~B_i~ are busy people. Alex has concluded that there are ~M~ such referrals that will happen. One person may refer Alex to multiple different people.

It is guaranteed that no cycles will occur, meaning you will not be referred to anyone a second time once you have already been referred to them.

It is also guaranteed that everyone on the list is reachable by forming a connection with just one person. (Since the people that Alex wants to connect to all have broad networks)

Alex is very shy, so he only wants to approach one person by himself. This person can be anyone on his list.

Assuming all connection wait times happen simultaneously (meaning you can have multiple connection wait times being processed at the same time), and that the first person that Alex connects to (the one that he approaches by himself) takes no waiting time, what's the shortest time needed for Alex to connect with every person on his list?

Note: Python users are recommended to use PyPy 2/3 over Python 2/3 when submitting.

Constraints

For all subtasks,

~2 \le N \le 5 \times 10^5~

~M < N~

~1 \le A_i, B_i \le N~

~1 \le C_i \le 10^9~

Subtask 1 [15%]

~2 \le N \le 100~

~1 \le C_i \le 10~

Subtask 2 [85%]

No additional constraints.

Input Specification

The first line of input will contain two space-separated integers, ~N~ and ~M~.

The next ~M~ lines will contain three space-separated integers, ~A_i~, ~B_i~ and ~C_i~.

Output Specification

Output one integer, the minimum number of days that Alex has to wait before he establishes a connection with everyone on his list.

Sample Input

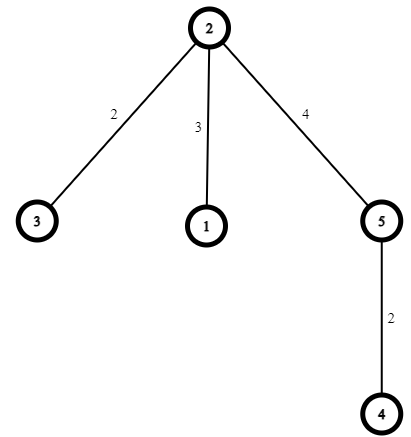
5 4
1 2 3
2 3 2
2 5 4
5 4 2

Sample Output

6

Explanation for Sample Output

If Alex approaches person 2, person 2 can refer him to persons 1, 3, and 5. After 4 days, person 5 connects with Alex (at this point, both person 1 and 3 have already connected with Alex), and refers Alex to person 4, who connects with Alex after 2 days. This entire process takes 6 days. This can be proven to be the most optimal solution.