Sandy the Squirrel has hit the jackpot by discovering that a secret golden walnut exists in one of the walnut trees that she frequents.

The walnut tree in question is composed of ~N~ nodes numbered ~1~ to ~N~ that are fully connected by ~N - 1~ branches. In her search, Sandy will start at node ~1~ and find the golden walnut at one of the ~N - 1~ other nodes. Then, she must then get back to node ~1~ to use the teleporter that she hid there.

After finding the treasure, Sandy will alert ~M~ other squirrels positioned at distinct starting nodes on the tree that will attempt to yoink it from her. At the start of every second, she will move to the next node on the simple path to node ~1~. At the end of every second, each of the ~M~ squirrels may move to any adjacent node or stay where they are. Multiple squirrels may occupy the same node. If, at any point in time (including the start), Sandy is on the same node as another squirrel, they will yoink the treasure. As soon as Sandy is on node ~1~ without any other squirrels there, she will be able to teleport away.

Since Sandy doesn't know the node that the golden walnut is located on, she would like you to help her find the number of nodes that it could be on such that she can make it back safely even if all the squirrels move optimally.

Constraints

~1 \le N \le 5 \cdot 10^5~

~1 \le M \le N~

Subtask 1 [20%]

~M = 1~

Subtask 2 [80%]

No further constraints.

Input Specification

The first line of input will contain two space-separated integers, ~N~ and ~M~.

The next ~N - 1~ lines will each contain two space-separated integers, ~u_i~ and ~v_i~ ~(1 \le u_i, v_i \le N)~, the two nodes that the ~i~th branch joins.

The next ~M~ lines will each contain one integer, ~w_i~ ~(1 \le w_i \le N)~, the starting location of the ~i~th squirrel.

Output Specification

Output one integer, the number of nodes that the golden walnut could be hidden on such that Sandy can make it back safely.

Sample Input 1

7 1
1 3
2 6
3 4
3 5
5 6
4 7
7

Sample Output 1

3

Explanation for Sample Output 1

Sandy can make it back safely starting from nodes ~3~, ~4~, and ~5~.

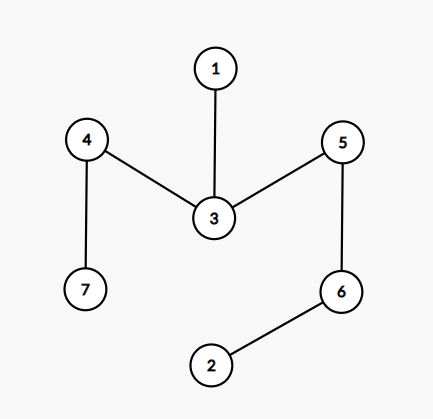
Sample Input 2

5 2
1 2
1 3
1 4 
1 5
1
4

Sample Output 2

0