The country of Beanland consists of ~N~ towns connected by ~M~ two-way roads. Mr. Bean, the leader of Beanland, has ordered each town to produce beans. Each town is ordered to produce a different type of bean, and these beans are then transported between towns. However, because the towns are far apart, it is possible the beans could spoil before reaching the next town.

Each road in Beanland has a length ~l_i~ and a start and end town, ~u_i~ and ~v_i~. All the towns in Beanland are guaranteed to be connected, meaning it is always possible to travel from one town to another along the two-way roads.

For each pair of two towns in Beanland, there is an optimal path. An optimal path is a path with the lowest sum of edge lengths. If the length of the optimal path is greater than ~K~, the beans will spoil in transport.

Mr. Bean, in order to save the beans, has a magical Bean Wand. If he waves the Bean Wand, he can reduce the length of all the roads by ~X~, to a minimum length of ~0~. However, he can only use this wand once. Mr. Bean would like to know what the smallest possible value of ~X~ is so that all beans can travel along the optimal path between any pair of cities without spoiling.

For this question, Python users are recommended to use PyPy in order to pass the time limit.

Input Specification

The first line of input will contain three space-separated integers, ~N (1 \leq N \leq 400)~, ~M (N-1 \leq M \leq 5000)~, and ~K (0 \leq K \leq 10^6)~, the number of towns, the number of two-way roads, and the maximum allowed optimal path length.

The next ~M~ lines of input will contain three space-separated integers each, ~u_i, v_i (1 \leq u_i, v_i \leq N)~, and ~l_i (0 \leq l_i \leq 10^6)~.

Output Specification

Output the smallest non-negative integer ~X~ that Mr. Bean can use without any beans spoiling in transport.

Subtasks

Subtask 1 [30%]

~N \leq 100~

~M \leq {N \choose 2}~

Sample Input 1

4 4 2
1 2 1
2 3 3
2 4 3
3 4 7

Sample Output 1

2

Sample Explanation 1

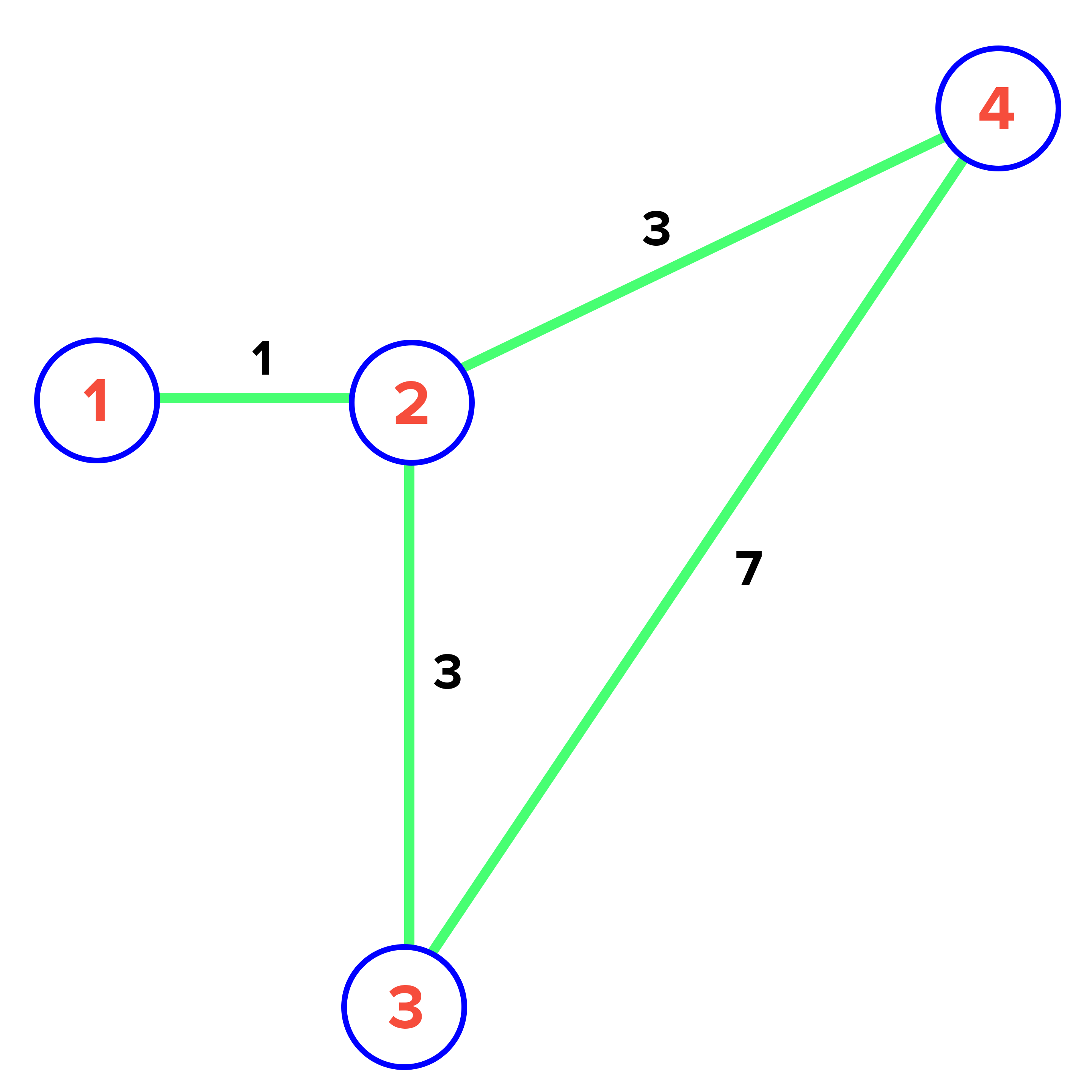
By setting ~K~ to ~2~, the edge from ~1~ to ~2~ equals to ~0~, ~2~ to ~4~ is equal to ~1~, ~2~ to ~3~ is equal to ~1~, and ~3~ to ~4~ is equal to ~5~. It can be determined that all of the optimal paths will now be ~2~ or less.

Sample Input 2

5 6 7
1 2 6
1 5 8
2 5 7
2 3 9
4 3 3
4 5 4

Sample Output 2

3