Rectangular Reckonings
View as PDFGiven a square, -indexed,
-d array of integers, of width and length
, and a separate set of
subarrays, find the sum of all the elements in the original array that are a part of exactly a single subarray.
Each subarray is described using two separate indices, the "top-left" index, and the "bottom-right" index. This system makes the most sense if you think about the array like a grid with at the top-left and
at the bottom-right. Each subarray can then be thought of as a rectangle that fits inside the grid.
Input Specification
The first line contains a single integer
, the size of both dimensions of the array.
The next lines will each contain
integers, the contents of the array. These integers will all be between
and
inclusive.
The next line contains a single integer the number of subarrays.
The next
lines will contain four integers
,
,
,
, the top-left indices followed by the bottom-right indices of a subarray.
It can be noted that for all subarrays and
.
Output Specification
A single integer, the total sum of all the elements that are only in subarray.
Subtasks
Sample Cases [10%]
Subtask 1 [20%]
Subtask 3 [70%]
No further restrictions.
Sample Input 1
4
1 2 3 4
5 6 7 8
9 1 1 0
1 3 5 1
1
1 1 2 3Sample Output 1
23Sample Input 2
4
1 2 3 4
5 6 7 8
9 1 1 0
1 3 5 1
2
1 1 2 3
2 1 3 3Sample Output 2
19Sample Visual
Here is the array that is used in both sample inputs, with the subarray 1 1 2 3 outlined in 2 1 3 3 outlined in
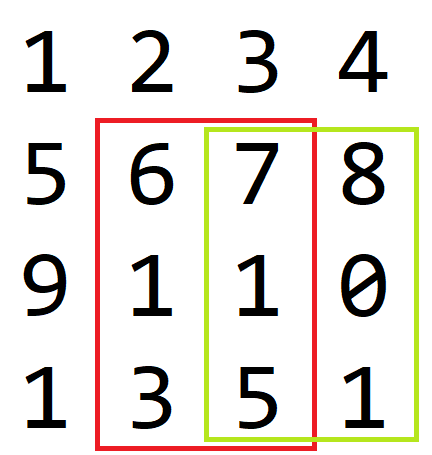
Comments