Given a tree with ~N~ nodes, find all centroid nodes in increasing order.

A centroid node is a node that, when removed, splits the tree into subtrees such that each subtree has ~\le \frac{N}{2}~ nodes.

Constraints

~3 \le N \le 2 \times 10^5~

Input Specification

The first line of input will contain ~N~.

The next ~N-1~ lines will contain ~2~ integers ~u~ and ~v \ (1 \le u, v \le N)~ denoting an edge between the two nodes.

Output Specification

On the first line, output the number of centroid nodes, ~C~.

On the next ~C~ lines, output the centroid nodes in increasing order.

Sample Input 1

4
1 2
3 2
4 3

Sample Output 1

2
2
3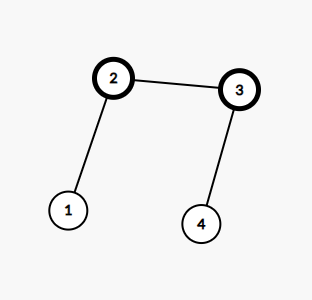

The two centroids are nodes ~2~ and ~3~.

Sample Input 2

10
1 2
2 3
3 5
3 6
3 7
2 4
2 8
8 9
9 10

Sample Output 2

1
2

Explanation for Sample Output 2

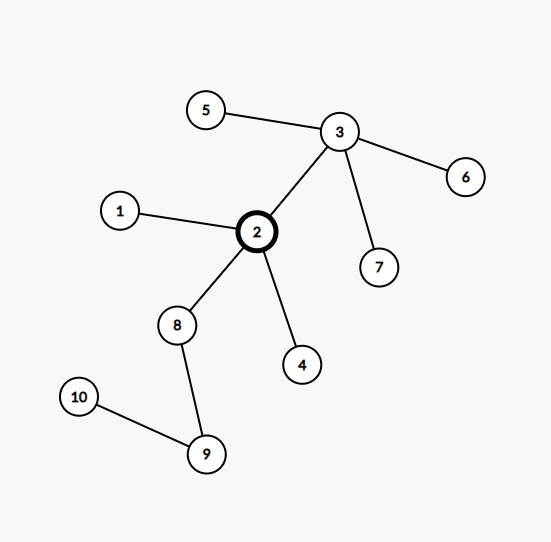
The only node that is a centroid is node ~2~.