Long before he starts to deliver any presents, Santa must take a test flight over each area he will fly over to make sure he knows what path he is going to take.

Traditionally, this path is in the shape of a triangle with vertices ~(x_1, y_1)~, ~(x_2, y_2)~, and ~(x_3, y_3)~. However, Santa's elves have recently suggested that he should take a circular path instead to maximize the area that the path surrounds (so he can see more of the environment below). Santa knows that he still has to pass through the three vertices and wants to figure out whether it will be worth it to change his flight path.

Santa asks you to report to him the area he will gain by traveling a circular path around the three vertices rather than a triangular path.

Input Specification

The first line will contain six space-separated real numbers, ~x_1~, ~y_1~, ~x_2~, ~y_2~, ~x_3~, and ~y_3~ ~(|x_1|, |y_1|, |x_2|, |y_2|, |x_3|, |y_3| \le 100)~. It is guaranteed that these points will make up a non-degenerate triangle.

Output Specification

Output one line containing a real number, the increase in the surrounded area if Santa takes a circular path.

Output your answer to ~6~ decimal places. Your answer will be considered correct if its absolute or relative error does not exceed ~10^{-6}~.

Sample Input

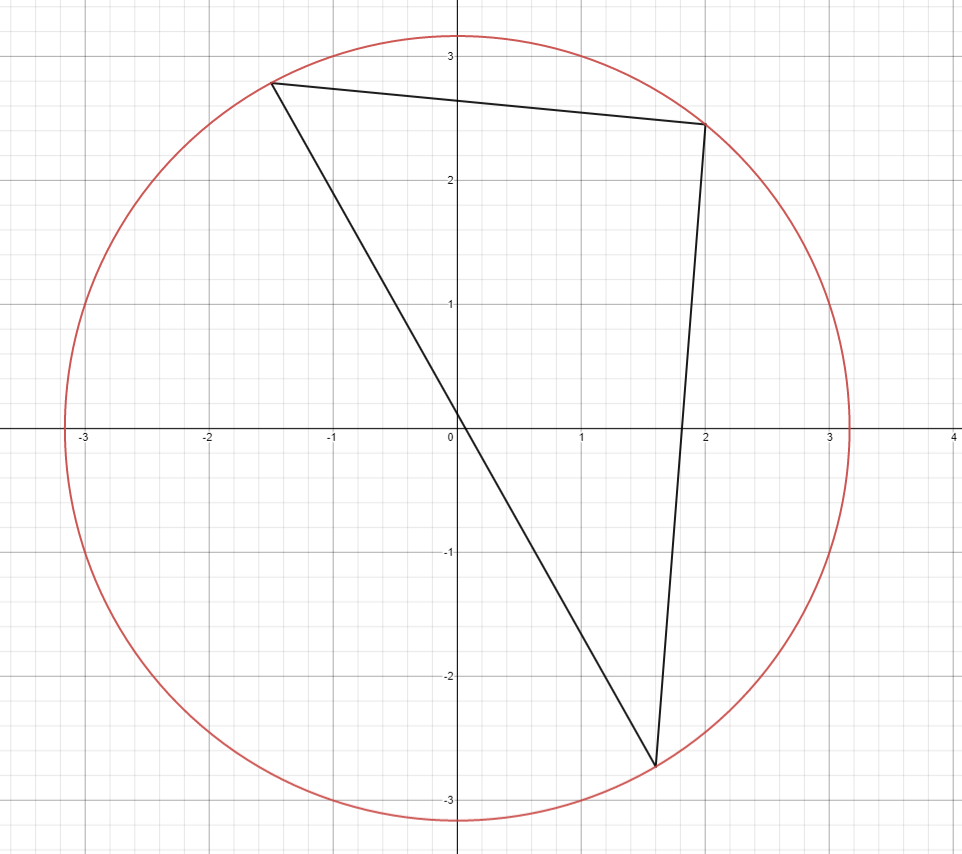
2.0 2.5 1.6 -2.7 -1.5 2.8

Sample Output

22.148359

Explanation for Sample Output

The following diagram depicts the circular path and the triangular path. The difference in area ends up being approximately ~22.148359~.